383. Гистограмма

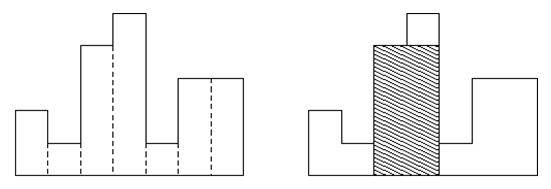
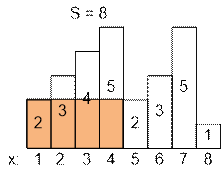
Гистограмма является многоугольником, сформированным из последовательности прямоугольников, выровненных на общей базовой линии. Прямоугольники имеют равную ширину, но могут иметь различные высоты. Например, фигура слева показывает гистограмму, которая состоит из прямоугольников с высотами 2, 1, 4, 5, 1, 3, 3. Все прямоугольники на этом рисунке имеют ширину, равную 1.

Обычно гистограммы используются для представления дискретных распределений, например, частоты символов в текстах. Отметьте, что порядок прямоугольников очень важен. Вычислите область самого большого прямоугольника в гистограмме, который также находится на общей базовой линии. На рисунке справа заштрихованная фигура является самым большим выровненным прямоугольником на изображенной гистограмме.

Вход. В первой строке записано число n (0 ≤ n ≤ 10⁶) – количество прямоугольников гистограммы. Затем следует n целых чисел h₁, ..., h_n (0 ≤ h_i ≤ 10⁹). Эти числа обозначают высоты прямоугольников гистограммы слева направо. Ширина каждого прямоугольника равна 1.

Выход. Вывести площадь самого большого прямоугольника в гистограмме. Помните, что этот прямоугольник должен быть на общей базовой линии.

Пример входа	Пример выхода
7 2 1 4 5 1 3 3	8

РЕШЕНИЕ

структуры данных - стек

Анализ алгоритма

Реализация за O(n²). Для каждого i-го прямоугольника ширины 1 постараемся раздвинуть его границы влево left и вправо right пока это возможно (то есть высоты всех прямоугольников от left-го до right-го не менее h_i, 1 ≤ left ≤ i ≤ right ≤ n). Получим максимально возможный прямоугольник, вписанный в гистограмму, который упирается в верх i-го прямоугольника. Среди всех таких прямоугольников ищем максимум. Решение дает Time Limit.

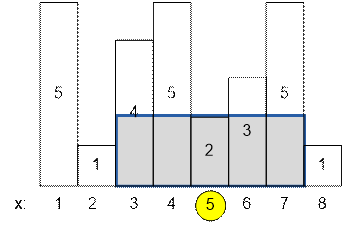
Впишем максимальный прямоугольник, упирающийся в верх 5-го прямоугольника. Его границами будут [left; right] = [3; 7], высота равна 2. Площадь равна (right – left + 1) * h₅ = (7 – 3 + 1) * 2 = 5 * 2 = 10.

Реализация за O(n). Каждый прямоугольник характеризуется абсциссой i и высотой h_i. Заведем стек из пар (i, h_i) – характеристик прямоугольников. Введем в рассмотрение два дополнительных прямоугольника с высотами h₀ = -1, h_n+1 = 0. Занесем нулевой прямоугольник с высотой -1 в стек (пару (0, -1) кладем в стек). Такие высоты выбраны для того чтобы:

· нулевой прямоугольник никогда не был извлечен из стека;

· обработка последнего прямоугольника с высотой 0 вытолкнет из стека все имеющиеся там прямоугольники кроме нулевого;

Пусть текущим является i-ый прямоугольник абсциссой i и высотой h_i. Тогда:

· Если его высота больше высоты прямоугольника на вершине стека, то заносим i-ый прямоугольник в стек.

· Пока высота текущего прямоугольника (i, h_i) меньше или равна высоте прямоугольника на вершине стека (x, h_x) (то есть h_i ≤ h_x), то извлекаем прямоугольник из стека и вычисляем площадь максимального вписанного в гистограмму прямоугольника. Подозрительным на максимальный будет прямоугольник со сторонами i – x (он начинается в абсциссе x и заканчивается в абсциссе i – 1) и h_x. Пусть последний вытолкнутый из стека прямоугольник ширины 1 имеет характеристики (j, h_j) (h_j ≥ h_i). Тогда в стек следует положить пару (j, h_i).

Пример

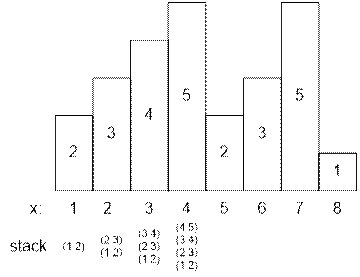
Пусть мы дошли до четвертого прямоугольника включительно. Поскольку до него высоты прямоугольников шли по возрастающей, то они добавлялись в стек. Следующий пятый прямоугольник имеет высоту 2. Последовательно извлекаем прямоугольники из стека, высоты которых строго больше текущего и пересчитываем площади получившихся максимальных прямоугольников:

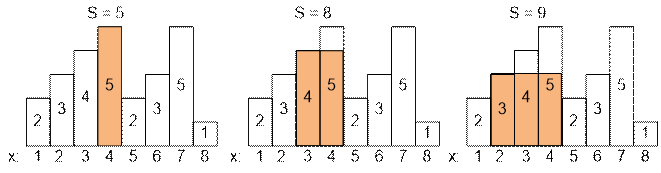
Пятый прямоугольник имеет высоту 2, извлекаем из стека первый прямоугольник, пересчитываем площадь:

В стеке остался только нулевой прямоугольник с высотой -1. Последний вытолкнутый из стека прямоугольник имеет характеристики (j, h_j) = (1, 2). Текущим рассматриваемым является прямоугольник номер 5 с высотой 2, то есть (i, h_i) = (5, 2). Следовательно в стек заносим прямоугольник с параметрами (j, h_i) = (1, 2). В дальнейшем состояние стека будет следующим:

Реализация алгоритма

В структуре Node будем хранить абсциссу x и высоту прямоугольника Height в этой абсциссе. Объявим стек s из этих структур.

struct Node

{

int x;

int Height;

Node(int x, int Height) : x(x), Height(Height) {};

};

stack<Node> s;

Читаем входные данные. Считаем высоты нулевого и (n + 1)-го прямоугольника равными соответственно -1 и 0. Занесем в стек нулевой прямоугольник. Поскольку его высота равна -1, то он никогда не будет вытолкнут из стека.

scanf("%d",&n);

s.push(Node(0,-1));

Последовательно обрабатываем прямоугольники. Площадь максимального покрывающего гистограмму прямоугольника подсчитываем в переменной res.

res = 0;

for(i = 1; i <= n + 1; i++)

{

Читаем высоту i-го прямоугольника. Его абсцисса x равна i. Если i = n + 1, то его высота равна нулю: в конце необходимо вытолкнуть все прямоугольники из стека кроме первого с высотой -1 и пересчитать искомую площадь.

if (i <= n) scanf("%d",&h); else h = 0;

int x = i;

while (h <= s.top().Height)

{

x = s.top().x; hPrev = s.top().Height; s.pop();

area = 1LL * hPrev * (i - x);

if (area > res) res = area;

}

s.push(Node(x,h));

}

Выводим площадь наибольшего прямоугольника.

printf("%lld\n",res);

Реализация за O(n²)

#include <stdio.h>

#define MAX 1000010

long long h[MAX];

int i, n, left, right;

long long area, res;

int main(void)

{

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&h[i]);

res = 0;

for(i = 1; i <= n; i++)

{

left = right = i;

while(left > 1 && h[left-1] >= h[i]) left--;

while(right < n && h[right+1] >= h[i]) right++;

area = (right - left + 1) * h[i];

if (area > res) res = area;

}

printf("%lld\n",res);

return 0;

}